Mo
05
Feb
2024
Squircle

Im Magazin der MAA (math.Assoc.America) bin ich auf die Squircles aufmerksam gemacht worden.
Der Name kommt von Squares to Circles.
Es ist ein Zwischending zwischen Quadrat und Kreis. Man kann dafür verschiedene Definitionen vorschlagen. Mir gefällt die einfachst beschreibbare. Eine Kurve, die die Gleichung |x|^p+|y|^p=1 erfüllt.
Ich habe für p die Werte zwei, goldener Schnitt, Euler Konstane e und Pi eingesetzt, um eine schöne Auswahl zu bekommen.
Dabei bin ich darauf gestossen, dass man danach fragen kann, was passiert, wenn man die Fläche dieser Kurve ausrechnet und sie als Parameter p einer weiteren Kurve verwendet.
Let squircle(p) be the curve satisfying the equation |x|^p+|y|^p=1
If F(p) := area of squircle(p)
then p=3.6619679144529437707549.. is a fixpoint of F.
F(p) = ∫[0,1] (1-x^p)^(1/p) dx *4
Ich habe diese Fixpointkonstante 3.66196.. (die man Baumann'sche Konstante nennen könnte) mit Maple bis auf 10'000 Stellen nach dem Komma berechnet (ca. 14 Tage PC 2.66 GHz CPU time).
Dabei ist hilfreich dass die Fläche oben elegant auf die Eulerfunktion B(x,y) zurückführbar ist.
So
04
Feb
2024
LaserBox

LaserBox ist für mich ein bisschen eine Kombination zwischen LaserTank und 15er Spiel.
Es ist eine App fürs Handy. Ich habe sie jetzt nach ein paar Jahren wiederaufgegriffen.
Man kann Tipps kaufen und damit das Spiel auf eine Verallgemeinerung des 15er Spiels reduzieren. Ich habe das gemacht, weil diese Verallgemeinerung äusserst anspruchsvoll sein.
In den bisher angetroffenen 100 Levels ist die Variante " 7x11 Gitter plus NUR ein Leerplatz" die schwierigste.
Weil seit 2014 täglich eine neue Aufgabe dazukommt, werde ich bis zu meinem 100sten Geburtstag 10'000 Levels begegnet haben (100^2).
Sa
03
Feb
2024
Künstliche Intelligenz Kunst

Chat-GPT hat letztes Jahr Furore gemacht. Dabei ist auch mit künstlicher Intelligenz unterstützte Kunst interessant.
Ich habe während ein paar Tagen mit civitAi.com herumgespielt. Man spürt dabei gut, wie der Hybrid Mensch-Maschine funktioniert.
Ich zeige ein paar Beispiele.
Mi
18
Okt
2023
Die Voronoizelle unserer Sonne

AlphaCentauri
Lacaille
Lalande
EpsEridani
61Cygni
Prokyon
Ross
Sirius
GroomBridge
epsIndi
Das sind die 10 nächsten Sterne unserer Sonne.
Man kann, indem man auf der Wegmitte zu jedem dieser Sterne eine zum Weg senkrechte unendlich ausgedehnte Wand errichtet, die Voronoizelle unserer Sonne bestimmen.
Es ist eine Art "Einzugsgebiet".
Weil die Sterne sich bewegen, ist es die Situation unserer Gegenwart.
Die Massen der Sterne habe ich vernachlässigt. Alle gleich massig wie die Sonne angenommen.
Es ist ein Polyeder mit 9 Flächen, 11 Ecken und 18 Kanten.
Der entfernteste Stern Epsilon Indi ist nicht mehr am Polyeder beteiligt.
Das Rechnen mit analytischer Geometrie erwies sich als kompliziert genug, dass ich es vorzog, mit einem beliebig verfeinerbaren Gitter zu arbeiten.
Jeder Gitterpunkt bekommt als Label den nächsten Stern. Die räumlichen Ecken des Polyeders sind dadurch ausgezeichnet, dass sie 4 verschiedene Labels in der Nachbarschaft haben.
Mi
06
Sep
2023
Orientierungslauf WMOC Slowakei

Orientierungslauf Senioren Weltmeisterschaft 2023 in Kosice Slowakei
Die Schweiz vor tausend Jahren. Sehr viel Wald, wenig Städte und Dörfer. Waldstrassen als grüne Tunnels. Nur von mir stark beachtetes Ziegelmuster einer Kirche in Kosice. Schöne Unterkunft mitten im Wald. Für den "LongFinal" : wunderschöner Dolinenwald.
Di
11
Jul
2023
Die Ebene mit Fünfecken kacheln, die ganzzahlig lange Seiten haben

Mit regulären Fünfecken kann man die 2-dimensionale Ebene NICHT kacheln (lückenlos und ohne Uebelappungen bedecken).
Mit unregelmässigen konvexen Fünfecke (Seiten und/oder Winkel) geht das aber. Immer mit demselben Typ von Kacheln.
Zu 14 seit längerer Zeit bekannten Kachelfamilien ist erst kürzlich eine letzte 15te gestossen.
In einer noch neueren Arbeit (MAA) ist die Frage nach Exemplaren mit GANZZAHLIGEN Seitenlängen gestellt worden. Das ist eine faszinierende Untersuchung. In der ganzen Arbeit wird aber kein einziges Exemplar gezeigt (nur Formeln).
Mit nicht geringem Aufwand habe ich ein solches produziert : 1, 9, 5, 5 und 10 in der Familie No 13.
Sa
08
Jul
2023
Aperiodic monotile

Für mich ist das Jahr 2023 das Jahr des Hutes !
Nachdem mich die Welt der Zweierkachel von Penrose und das Thema der Quasikristalle faszinieren konnten, ist in diesem Jahr die aperiodische Kachelung mit einer EINZIGEN Kachel entdeckt worden. Der "Einstein", wie er amüsanterweise auch genannt wird. Die Kachel hat die Form eines Hutes.
Der Artikel, der die Entdeckung beschreibt, ist sehr lang und nicht leicht zulesen. Hier.
Ich habe 105 3D geprintete Kacheln gekauft und mit grossem Vergnügen damit gespielt.
Es ist eine wahre Sensation, die wohl nur von einem Bruchteil der Weltbevölkerung wahrgenommen wird. Leider.
Do
23
Feb
2023
Spielen in 4D, MC4D

Nach meiner monatedauernden Beschäftigung im 4-Dimensionalen mit "Cubelikes" mittels des Programmes MPULT, habe ich mich jetzt dem Programm MagicCube4D MC4D zugewandt.
Hier interessieren mich Varianten mit möglichst wenig Unterteilungen und solche, die noch niemand gespielt hat.
Ein solches ist das Duoprisme 652 (Hexaprismenring plus Pentaprismenring plus 2er Unterteilung).
Während eines Monates bin ich immer wieder zu diesem 4D Puzzle zurückgekehrt und habe es mit Hartnäckigkeit aber viel Vergnügen fertig gelöst.
Di
21
Feb
2023
Prieur

Anlässlich eines im Internet angetroffenen Youtube-Zoomes zum galaktrischen Zentrum sind mir Konstellationen aufgefallen, die natürlich noch keinen Namen haben, weil es viel zu viele von ihnen gibt.
Trotzdem wollte ich Duzis machen mit ein paar von ihnen.
Es sind jetzt schon eine ganze Reihe.
♡ collier
♡ parabole
♡ prieur
♡ sourire (ed)
♡ sigma
♡ "abc" sous sourir
Bild 1
collier und parabole
Bild 2
prieur
Bild 3
sigma, sourire und abc
Es stellt sich heraus, dass es gar nicht immer leicht ist, den Vornamen der beteiligten Sterne herauszufinden.
Es gibt da eine natürliche Grenze für mich : der Horizont der Sterne in der App Stellarium. Das sind die Sterne mit DR2 und einer 19 stelligen Nummer.
Hier sind die Sternenamen der drei gut erreichbaren Konstellationen.
collier
1=DR2 405 760 699 353 844 9664
2=DR2 405 751 316 139 667 6608
3=DR2 405 751 308 837 401 4592
4=DR2 405 751 305 831 745 5488
5=DR2 405 751 305 401 375 2936
6=DR2 405 751 295 093 502 3232
7=DR2 405 751 291 657 527 4624
8=DR2 405 751 260 733 763 2000
9=DR2 405 751 281 349 607 2320
parabole
1=DR2 405 752 507 992 561 4080
2=DR2 405 752 511 858 575 7440
3=DR2 405 752 532 474 419 0720
4=DR2 405 752 532 474 419 3152
5=DR2 405 752 542 352 305 3440
6=DR2 405 752 549 224 238 6688
7=DR2 405 752 851 589 955 9680
8=DR2 405 752 862 327 911 8720
9=DR2 405 752 861 897 880 2560
prieur
Gaia DR2 405 748 ...
1 : ...182 531 460 5312
2 : ...182 101 259 2512
3 : ...182 101 259 2768
4 : ...182 530 701 2508
5 : ...182 101 259 2640
6 : ...175 229 311 5648
7 : ...175 659 512 4096
Jenseits dieser Grenze wird es dann deutlich schwieriger die Namen rauszufinden. Man muss auf spezielle Datenbanken im Internet zugreifen und sich mit Koordinatensystemen und Filter herumschlagen.
"Sourire" war mir im Zoom aufgefallen und ich hatte bald ein gutes NACO Bild von ihm.
Hier sieht man "Sourire" im schon unscharfen "Prieur".
Bild 4
In der Zwischenzeit habe ich (dank Lucien) die Namen für "Sourire"
1 = GCIRS 16NE
2 = GCIRS 16CC
3 = GCIRS 16C
4 = GCIRS 16NW
GC steht für galactic center
IR für infra red
S für search.
Bild 5
So
19
Feb
2023
Turing

Eventuell als Blog-Item
Turing kennen wie alle als Informatiker und Knacker der Enigma Maschine.
Aber haben wir seinen Turing Rechner "erlebt" und "gefühlt" ?
Es ist ein Computer, der auf ein Minimum von Bestandteilen reduziert ist und vielen fast philospphischen Betrachtungen dient.
Ich jedenfalls nicht bevor mich jemand auf die App "The Turing Game" (nicht verwechseln mit Turing Test Game) aufmerksam gemacht hat.
Es lohnt sich unbedingt, damit Stunden zu verbringen.
Es gehört auf jedes "anständige" Android Handy !
Es hat 15 Aufgaben mit zunehmender Schwierigkeit.
Die letzte Aufgabe habe ich mit 66 Karten (=Zustände) gelöst.
Eine sehr wichtige Entdeckung, die ich machen musste, ist folgende. Beim Behandeln einer Reihe von Objekten muss man früh erkennen, dass es das letzte ist und entsprechen anders handeln, um nicht in die unendlichen Bandenden zu geraten.
Hier kann man der Maschine zuschauen ! Hier
Sa
31
Dez
2022
Pneu's packen

"Geschüttete" Pneu's scheinen sich kreuzweise lagern zu wollen.
Wenn ich von Pneu's auf Tori wechsle, entsteht daraus ein interessantes mathematisches Problem. Was sind die höchsten Füllgrade bei den Tori ?
Ein Torus hat zwei Parameter, der Radius r des Profils und der Radius R des Ringes.
Ich habe mir zunächst den recht rundlichen Fall von R/r=1 vorgenommen und eine Referentstapelung RS wie folgt vorgenommen.
Die Tori zu senkrechten Türmen stapeln. Diese Türme bienewabenmässig zusammenstellen. Dann jede zweite Diagonale in diesem Muster um r anheben, was eine platzsparende Verzahnung ermöglicht.
Weil man jeden Torus in eine zylindrische Hülle stecken kann, die er mit einem Füllgrad FG1 ausfüllt, kann den Gesammtfüllgrad FG auf drei Faktoren zurückführen : FG1, dann der Füllgrad der Kreise im 2D und schliesslich den Gewinnfaktor durch die Verzahnung.
Das ergibt zusammen die bestechend einfache Formel
FG = (1/WURZEL(3)-1/2)*Pi^2
Das sind 76%+, die wir mit den 74%+ der dichtesten Kugelpackung vergleichen können.
Obwohl bei einer alternativen, kreuzweisen Stapelung ein Torus in die Hülle seines Nachbarn eindringen kann, was ohne Frage ein Gewinn wäre, glaube ich nicht, dass netto ein Gewinn bleibt, weil man eine damit verbundene Spreizung nicht vermeiden kann.
Damit vermute ich das RS optimal ist.
Man kann kann auch einen geschlossenen Ausdruck des RS-Füllgrades in Funktion des Torusformates R/r etablieren (1).
Tadeusz Dorozinski hat schon 2014 eine Füllung des Raumes mit Tori vom Format 3.41+ publiziert, bei der die Tori miteinander verhänkt sind, dh. Es gehen je 4 Tori durch das Loch eines anderen Torus. Das Herausfinden des Füllgrades dieser Anordnung ist eine hübsche Aufgabe. Man kann abzählen, dass 6 Tori in einer kubischen Elementarzelle vorhanden sind (je ein halber Torus für die 6 Seiten und je ein Vierteltorus für die 12 Kanten).
Es ergibt sich die schlichte Formel
FG = 6*Pi^2 * (29*Wurzel(2)-41).
Das sind 72%+.
Weil die RS Familie gemäss (1) Füllgrade bis 76%+ hat, kann man fragen, für welches Format der Tori gegebene Füllgrade erreicht werden.
Format R/r = 1.41835+ gibt den Füllgrad 74%+ der dichtesten Kugelpackung.
Format R/r = 1.60672+ (nahe am goldenen Schnitt 1.618+) gibt den Füllgrad 72%+ der Doro-Packung.
Bei der Doro-Packung gehen vier Tori durch jedes Torusloch. Man könnte nur je zwei Tori verlinken und das Format R/r=2 wählen, sodass jedes Torusloch durch einen Torus gefüllt wird. In diesem Falle kann man einen Füllgrad von 60%- erreichen.
Wenn man dieses Format R/r=2 in die Referenzstapelung RS nimmt, also das Torusloch nicht stopft, bekommt man einen besseren Füllgrad, nämlich 67%+ (fast genau 2/3) statt 60%-.
Füllgrad für Pillen
Wenn man bei der dichtesten Kugelpackung die Kugel r halbiert und dazwischen einen Zylinder der Höhe h einfügt erhält man eine Art Pillen mit dem Format f=h/r. Mit f verändert sich der Füllgrad. Bei f=0 haben wir den Füllgrad 74%+, der dann für f gegen unendlich sich dem Wert 90%+ annähert.
Mo
12
Sep
2022
Bergtourg Gros Perré, Sommer 2022

Eine weitere Etappe in der Erkundung der Vanil Noir Kette.
https://www.hikr.org/tour/post173746.html
So
11
Sep
2022
GinGin, Sommer 2022

Eine sehr bemerkenswerte mathematische Konstante.
Ich hatte noch nie etwas von der *Chintschin Konstante* gehört.
Jede irrationale Zahl kann in einen Kettenbruch umgewandelt werden.
Das geometrische Mittel der Kettenbruchzahlen ist eine Konstante !!! Unabhängig von der gewählten irrationalen Zahl. Das ist ENORM erstaunlich.
Sie ist bemerkenswert und ich habe mir die Mühe genommen, ihre 10., 100. , ... millionste Nachkommastelle auf Internet herauszufinden.
Chintschin Konstante = 2.6854520010..
Die millionste Stelle ist eine 1
Die 100'000ste Stelle ist eine 9
Die 10'000ste Stelle ist eine 7
Die 1'000ste Stelle ist eine 3
Die 100ste Stelle ist eine 9
Die zehnte Stelle ist eine 0
Sa
10
Sep
2022
Gravur T5 und Hp6, Herbst 2022

Da mein Freund Werner Straumann über ein professionelles Lasergraviergerät verfügt, ergab sich die Möglichkeit, Bilder meiner Seifenblasenfälle T5 und Hp6 mit hauchfeinen Linien herzustellen.
Fr
09
Sep
2022
Grammont

Bergtour auf den Grammont über dem Genfersee, hoch über dem Schloss Chillon.
Do
08
Sep
2022
Weitere Etappe für « 4D Kuboide »

Ein besonders langer Fall : 3x3x4x4
295'549 Züge.
Elapsed time : 210 Tage
Nach 250'000 Zügen erkannte ich ein Paritätsproblem, das mich 45'000 zusätzliche Züge kostete. Ich habe gelernt, dass man die Parität früher messen und damit die Kosten geringer halten kann. Man muss die Permutation der Mischung herausfinden. Dann ist die Parität gerade genau dann, wenn die Anzahl der geraden Zyklen gerade ist.
Siehe auch : https://edu1618.jimdofree.com/2022/05/24/4d-kuboide/
Mi
07
Sep
2022
AZ Oddly Triangular 2022

Gesucht eine möglichst grosse Zahl n mit lauter ungeraden Ziffern so, dass auch Triangular(n) nur ungerade Ziffern hat.
Ausgangspunkt war eine bisher bekannte grösste Lösung mit 34 Ziffern.
Der Wettbewerb degenerierte sehr schnell, als entdeckt wurde, dass man mit Mustern arbeiten kann, die Lösungen bis über 3 Mio Ziffern erlauben.
Mo
05
Sep
2022
AZ Stepping Stones, Sommer 2022

Ein weiterer Wettbewerb von AlZimmerman, an dem ich mit Vergnügen teilnehme.
So
04
Sep
2022
OL 3AG, Sommer 2022

Der traditionelle 3-Tage OL im Aargau, den ich seit vielen Jahren regelmässig besuche.
Sa
03
Sep
2022
OL Sanetsch & Klettern (Patou), Sommer 2022

Ein ganz besonderes OL Weekend im spektakulären Karst von Sanetsch.
Am Vortag Freitag habe ich den Klettergarten von Sanetsch kennengelernt und dabei eine etwas unfreundliche Begegnung mit zwei Patous gemacht.
Fr
02
Sep
2022
OL Apulien im Sommer 2022

OL Weltmeisterschaften für Senioren in der wunderbar kühlen Foresta Umbra von Gargano in Apulien. Die Sprints in den mittelalterlichen Dörfern waren sehr romantisch.
Do
01
Sep
2022
OL Arosa 2021

Wunderschöne OL-Woche in Arosa im Sommer 2021. https://www.swiss-o-week.ch/en/about-us/geschichte-en/716-2021-arosa-en
Für mich besonders erinnerungswert war die Hörnli-Abfahrt mit dem Velo am Ruhetag.
https://youtu.be/dh7_Vq1KS_Y?list=TLGG9jwB3DCu3rYxNjA5MjAyMg
Fr
01
Jul
2022
Rubesch

Rubesch steht für
Rubik Escher.
Rubik ist der klassische Rubik Würfel.
Escher ist der holländische Künstler, der für irritierende Geometrien bekannt ist und im Buch von Hofstaetter "Gödel, Escher, Bach" geehrt wird.
Marc Ringuette hat in der 4D Diskussionsgruppe auf einen Youtubefilm aufmerksam gemacht und anregende Betrachtungen dazu gemacht.
Ein gefundenes Fressen für mich, davon eine Simulation in Exel zu machen. Das gelang bestens und ich hatte eine gute ganze Woche Spass an einem deutlich erschwerten Puzzle, weil in meiner
Simulation natürlich alle 99 Etiketten einen individuellen Namen bekamen.
Interessant in diesem Zusammenhange ist, dass in meiner Exel Version 2003 unter Betriebsystem XP ein Zug 1 Sekunde dauert und dass im heutigen Exel unter Windows 10 der gleiche Zug hundert mal
länger dauert. Es ist den Microsoft Programmierern nicht gelungen, die Kompatibilität bez. VB Macros aufrecht zu erhalten (ein auf Internet bestens bekanntes Problem).
Ich habe das Puzzle in 1892 Zügen gelöst und zeige die letzten 44 Züge im zweiten Film hier.
Im Originalfilm sieht man die irritierende 3D Darstellung mit einem Grossteil, der nicht sichtbar ist, während in meinem Film mit der 2D Abwicklung alles sichtbar ist.
Mo
13
Jun
2022
Die Narbe des Chaumont

Di
24
Mai
2022
4D Kuboide

Rubik im Vierdimensionalen
Zur Popularisierung siehe Mathologer
Andrey Astrelin, der leider sehr jung verstorben ist, hat uns das sehr elegante Programm MPUlt hinterlassen, bei dem in wenig Zeilen eigene 4D Puzzles hinzugefügt werden können.
Mir ist folgende Familie von fünfzehn 4D-Puzzles aufgefallen, die ich hinzugefügt habe und die ich eins nachdem andern lösen will. Für zehn der fünfzehn habe ich das bereits getan. Auf die fünf
verbleibenden freue ich mich.
Es handelt sich um die Rubikwürfelähnlichen, bei denen die Unterteilungen zwischen zwei und vier liegen, zum Beispiel das
2x3x4x4.
In den Bildern stehen in je einer Kolonne die 8 Zellen der Würfelvariation im Vierdimensionalen.
Sa
21
Mai
2022
Pérollesbrücke

Di
08
Feb
2022
Eine 4-dimensionale Variante des Rubikwürfels : 2x2x2x3

Vor etwa 10 Jahren habe ich den 4-dimensionalen Rubikwürfel 3x3x3x3 gelöst und mich als 132. in eine Hall of Fame eintragen lassen. Heute sind dort 466 Leute eingetragen.
Melinda hat für die 4-dimesionale 2x2x2x2 Variante ein ganz und gar erstaunliches 3-dimensionales Modell mit Magneten erfunden, das nächstens nach ca 6 Jahren in Massen produziert werden soll. Siehe hier.
Jetzt hat jemand anders ein 3-dimensionales Modell für die 4-dimensionale Rubik Variante 2x2x2x3 geschaffen. Man beachte die wichtige 3 am Schluss.
Die 4-dimensionalen Rubiks kann man auf dem Rechner virtuell spielen. Da habe ich jetzt während ca einer Woche die Variante 2x2x2x3 durchgespielt. Ich habe 2047 Züge benötigt.
Sa
08
Jan
2022
niTiNol

Was ist ein niTiNol?
Die Teile ni und Ti im Namen stehen für Nickel und Titan. Es ist eine Metallegierung, die ein Erinnerungsvermögen hat ! Es ist ein dünner Draht, der als Transmissionsriemen zwischen zwei Rädern läuft. Er ist weich. Wenn er durch heisses Wasser läuft, wird er hart und streckt sich. Er erinnert sich an eine gestreckte Form, die man ihm bei ca 500 Grad eingebläut hat. Man kann den Motor als flachen Kit im Format A4 kaufen und zusammenbasteln. Wie der Streckwille des Drahtes ein Drehmoment erzeugt, zeige ich in einer Skizze.
Sa
08
Jan
2022
Der zweite Wettbewerb von AlZimmermann im Jahre 2021

Der zweite Wettbewerb von AlZimmermann im Jahre 2021
Diesmal ging es um mittelpunktsfreie Linien im trilinearem Gitter.
Das entsprechende 1-dimensionale Problem ist auf Internet gut abgehandelt und ich konnte diese Kenntnis geschickt ins 2-Dimensionale erweitern und damit 15 von 25 möglichen Punkte holen und zwar
OHNE Programmierung in diesem Programming Contest.
http://azspcs.com/Contest/APMath
Fr
20
Aug
2021
Col des Chamois

Sehr schöne Wanderung in der Gegend des Petit Muveran (Pont de Nant). Wegen das relativ kalten Sommers 2021 : wunderbarer Bergfrühling im Spätsommer!
So
15
Aug
2021
AlZimmermann Wettbewerb 2021

In einem vollständigen Graphen bei 3 Kantenfarben möglichst wenig gleichfarbige Dreiecke tolerieren. Der Wettbewerb verläuft etwas ungewöhnlich, weil 71 von 140 Teilnehmern die Maximalpunktzahl 25 erreicht haben.
http://azspcs.com/Contest/Cliques
So
04
Apr
2021
Gleichkantig machen

Vorläufiger Abschluss meiner Arbeiten in Sachen Gleichkantigmachen von Near Misses. Unter anderem hatte ich mir vorgenommen die Familie der Johnson Near Misses zu behandeln. Ich konnte effektiv alle 31 ausser einem (die Nummer 24) gleichkantig machen.
Melinda Green hat sich anerboten, das Resultat auf ihrer Webseite zu präsentieren.
So sieht das aus:
So
21
Feb
2021
59 Tetraeder

- Die Liste der 5 platonischen Polyeder
- Die Liste der 17 Kachelungen der Ebene mit Fünfecken
- Die Liste der 26 sporadischen Gruppen
- Die Liste der 59 Tetraeder mit rationalen Diederwinkeln
Vortrag (ppt)
https://combgeo.org/wp-content/uploads/2020/12/CGD-III-Alexander-Kolpakov.pdf
Artikel
https://math.mit.edu/~poonen/papers/space_vectors.pdf
Quantamagazin
Oben könnt Ihr in einem der 59 Tetraeder den Diederwinkel 120° sehen.
Unten unter mehr lesen folgen noch vom gleichen Tetraeder die Diederrwinkel 90°, 72° und 36°.
Do
24
Dez
2020
Johnson Near Misses

Bei meinem aktuellen Hobby, kleine Polyeder mit wenig Fazetten, die nur fast richtig sind ( near misses ) und die erst seit wenigen Jahren bekannt sind, durch opfern von gleichmässigen Winkeln zu reparieren (gleichkantig zu machen), bin ich auf die Familie der Johnson Near Misses gestossen.
Die unter dem Namen Johnson bekannten Polyeder werden mit gleichmässigen Polygonen aufgebaut. Es gibt nur 92.
Ich kürze im folgenden Johnson Near Misses mit "NmJ" ab.
Die ganze Liste von 31 Elementen könnt Ihr hier sehen http://www.orchidpalms.com/polyhedra/acrohedra/nearmiss/jsmn.htm
Es ist nicht so, dass meine geplante Reparatur immer gelingen kann. Ich habe hier schon einmal von einem Fall berichtet, wo diese Reparatur nur teilweise gelingt und habe das auch begründet.
Jetzt zeige ich 6 neue gelungene Fälle (no 1,3,4,5,7,11) und einen (no 8), bei dem man den Nachweis erbringen kann, dass es nicht geht. Weiter zeige ich zwei Fälle (no 9 und 10), von denen ich sehr stark vermute, dass sie nicht gehen.
Unten "mehr lesen" drücken, um sie alle sehen zu können. Zuerst die 6 gelungenen und dann die 3, die nicht gehen.
Die gerechneten Koordinaten (off-Dateien) der raparierten NmJ sind hier verfügbar
Mi
23
Dez
2020
Falkenflue

Di
22
Dez
2020
FAHI und TAHI

Mo
09
Nov
2020
Fortsetzung II beim Gleichkantigmachen von NearMisse-Polyedern

Ich habe noch zwei Polyeder mit wenig Seiten, deren Kanten nicht alle ganz gleich lang waren (NearMisses), durch Opfern von gleichmässigen Winkeln reparieren können.
Es sind zwei Acrohedron's, die Ecken haben, an denen zwei Fünfecke und ein Viereck zusammenstossen, also vom Typ 554. Variante A und Variante B.
Bei Variante A musste ich im Pentagon folgende von 108° abweichende Winkel einstellen: Scheitel 110.832°, Basis 105.722° und Seite 108.862°. Der spitze Winkel in der Raute ist 88.4357° (also kein Quadrat 90°).
Bei Variante B musste ich im Pentagon folgende von 108° abweichende Winkel einstellen: Scheitel 111.996°, Basis 109.209° und Seite 104.794°. Die Raute hat einen spitzen Winkel von 60°.
Jetzt sind es perfekte Gleichkanter. Weltneuheit.
Hier wird das erste Acrohedron Acro554A gezeigt.
Unter "mehr lesen" kann man auch das zweite Acrohedron sehen (Acro554B).
Do
01
Okt
2020
Fortsetzung beim Gleichkantigmachen von NearMiss-Polyedern

Bei der Nummer 7 (tripentagonal snub dodecahedron) habe ich schon mehrmals aus Mangel an Ausdauer aufgegeben.
Diesmal bin ich von den tetradrisch angeordneten Kappen aus je 3 nicht regelmässigen Pentagonen ausgegangen. Diese Pentagone müssen natürlich Lateralsymmetrie haben. Kennzeichnend ist der Scheitelwinkel, der eben von 108° abweicht. Es zeigte sich schnell, dass er etwas grösser sein muss, wenn die Gleichkantigkeit verbessert werden soll.
Neben dem Pentagonscheitelwinkel gamma habe ich noch zwei weitere Parameter im Modell. Die Distanz der Kappen voneinander sepa (wie Separation) und der Verdrehungwinkel alfa. Verdrehung wie bei den Snubs.
Es erweist sich, dass eine gewisse Raute entweder nach der kleinen oder der grossen Diagonale einknicken kann. Das ist der entscheidende Moment. Gleichkantigkeit kann ENDGUELTIG nicht erreicht werden. Der Fehler kann nur von 0.04802 um ca 11% auf 0.04261 reduziert werden!
Die optimalen Parameter sind
- gamma = 110.75°
- alfa = 42.4° und
- sepa = 3.170
Bei sepa = 3.170 ist die Kappenspitze 1.941 von der Polyedermitte entfernt.
Do
01
Okt
2020
Savolaires und Zulgbach
Mi
09
Sep
2020
1000m Klettersteig

So etwas macht man nicht mit 77 Jahren. Doch, doch! Und es machte wirklich Spass.
https://www.hikr.org/tour/post156669.html
La via ferrata compte 216 mètres d’échelles, plus de 2000 mètres de câbles et requiert une très bonne condition physique. Elle s’étend au-dessus de Loèche-les-Bains sur les falaises majestueuses du Daubenhorn. Pour atteindre le sommet du Daubenhorn (2941 mètres d’altitude), 8 heures et 1000 mètres de dénivellation vous attendent.
Mo
24
Aug
2020
Farbiges zählen mit Burnside

Mo
20
Jul
2020
Petit Muveran

Heute habe ich meinen langjährigen Traum wahr gemacht. Das ausnehmend schöne Matterhorn im Unterwallis, nämlich den Petit Muveran zu besteigen (mit kleinem Abstrich).
Di
09
Jun
2020
TchiSla

Nan Ma aus Amerika hat mich auf TchiSla aufmerksam gemacht. Es ist eine App für Apple-Handys, die süchtig machen kann. Es geht darum eine gegebene Zahl mit lauter gleichen Ziffern aufzubauen (möglichst wenige), wobei nur die Operationen +, -, *, / , Wurzel, Fakultät und Juxtapposition erlaubt sind. Ich zeige ein paar Juwelen.
Mo
08
Jun
2020
Roma versus Friburgo

Auf einer Internetplattform (PandaNet) hat der Go-Klub Fribourg gegen den Go-Klub von Rom gespielt. Die Begegnung wurde auf einem lokalen Fernsehsender ausführlich kommentiert.
So
07
Jun
2020
Der Wettbewerb von Tadeusz Dorozinski, animierter Nachtrag

Für die Präsentation der Lösungen unseres Wettbewerbs stellte ich mir Animationen vor. Solche mit CAD Programmen zu realisieren (wie Blender) ist nicht trivial. Da kam mir entgegen, dass es auf Internet Programme für virtuelle Origami (Faltkunst) gibt. Für die hier gezeigte Animation konnte ich ein solches in Anspruch nehmen.
Sa
25
Apr
2020
Der Wettbewerb von Tadeusz Dorozinski, Nachtrag

- das Hexa-Pyramiden-Kissen (Kooperation Tadeusz & ich) : Sieger, Volumen 120 cm3
- mein Kissen von 1974, abgeändert durch Tadeusz, Volumen 116 cm3
- mein Kissen von 1974, Volumen 115 cm3
- eine Variante des Hexa-Pyr-Kissens (2), Volumen 113 cm3
Di
21
Apr
2020
Bildverwackelungstechnik

Stichworte
openSimplexNoise (Bibliothek), Perlin, Entwicklerumgebung processing.exe, Skript ausführen, Lerp.
Do
16
Apr
2020
Der Wettbewerb von Tadeusz Dorozinski

Tadeus Dorozinski aus Düsseldorf hatte die glänzende Idee, auf FaceBook zu einem Wettbewerb aufzurufen, der zu erstaunlich viel sehr verschiedenen Antworten führte. Es geht darum, aus einem quadratischen Stück Papier 12cm mal 12 cm nur durch Falten und Wegschneiden von Unerwünschtem ein Maximum von Volumen zu erreichen, wobei das Stück Papier nicht in zwei oder mehr Teile zerfallen darf. Ich zeige in den Bildern die eingereichten Vorschläge, geordnet nach abnehmendem Volumen. Die genauen Koordinaten können bei mir nachgefragt werden.
Fr
31
Jan
2020
Kleine Fast-Gleichkanter (Polyeder) gleichkantig machen

NearMisses, konvexe Polyeder mit lauter fast gleichlangen Kanten, dadurch korrigieren, dass von den immer gleichen Innenwinkeln in den Polygonen abgewichen wird, ist eine sehr interessante Aufgabe.
Das ist deshalb nicht trivial, weil bei n-eckigen Seiten des Polyeders mit n>3 diese n Ecken sehr leicht nicht mehr in einer Ebene liegen.
Ich arbeite jeweils in einer Exel Datei und formuliere die Aufgabe mit analytischer Geometrie derart, dass der exelinterne Solver mobilisiert werden kann.
Ich interessiere mich für „kleine“ NearMisses, d.h. solche mit wenig Fazetten.
Die Illustration zeigt die drei Parameter bei der Behandlung von NearMiss No 3.
Unten könnt Ihr drei erfolgreich transformierte Beispiele in Animation sehen.
- nm5
- nm6
- nm3
Die erste Liste von 11 NearMisses ist
- 1_38-faces
- 2_28-faces
- 3_50_QTT4H3_w4
- 4_68_-snub-exp tet dodecahedron
- 5_32_QTT4H3_w4_redu
- 6_26-curvy octahedroid
- 7_tripentagonal snub dodecahedron_konvex-false
- 8_68-faces
- 74-near-miss
- 10_16-c28w5
- 7_40-P4-snub...
Liste von anderen Listen
- Erste Liste mit 11 Elementen
- GreatStella mit 5 Elementen
- Mobil GreatStella mit 6 Elementen
- Orchipalms/acrohedra/nearmiss mit 31 Elementen
Mi
29
Jan
2020
Dolinen im Kanton Fribourg

Di
28
Jan
2020
Mega Magic Tile

MagicTile ist ein zum Spielen mit virtuellen rubikwürfelähnlichen "Farbverdrehern", das ich hier schon öfter präsentiert habe. Im Programm kann man über tausend verschiedene Spiele auswählen. Ueber die diesjährigen Feiertage habe ich mir ein besonders grosses Spiel ausgewählt, das noch nie jemand gelöst hat. Mit viel Geduld und grosser Disziplin war ich rund 30 Tage mit 2 Stunden pro Tag mit diesem Spiel beschäftigt und habe über eine Million Züge gemacht. Es hat 42 verschiedene Farben und 9 Typen von Teilchen, die alle "nach hause" gebracht werden müssen.
Bild mit einer Drehung 2mal
Bild mit den 9 Typen.
Zeitgeraffter Film https://www.youtube.com/watch?v=nDYd7xdPRdE
Di
22
Okt
2019
Die Stacheligen

Tadeusz Dorozinski hat folgende wunderschöne Spiraldeltaeder erfunden.
https://geometryka.wordpress.com/2019/09/
Dabei werden bei einem Doppeltetraeder zwei benachbarte Dreiecke weggenommen, wodurch ein Art beweglicher Schnabel entsteht. Die Oeffnung dieses Schnabels kann man mit meiner Formel geeignet wählen, sodass die Schnäbel sich perfekt an den Antiprismenturm anschmiegen. Meine Formel ist folgende.
Mi
11
Sep
2019
Die zwei Bachwanderungen in diesem Jahr 2019

Der Schwandbach, ein Zufluss zum Schwarzwasser, mit Werner Straumann
Der Rüdigraben, ein Zufluss zur Aergera, allein.
Mo
19
Aug
2019
AlZimmerman programming contest 2019

Inverting Nearness = Die Nachbarschaftsverhältnisse umkehren. Was nahe ist, soll ferne sein und umgekehrt, auf einem Torus. Faszinierender Wettbewerb, bei dem etwa 300 Teilnehmer mitmachen und der bis Oktober dauert.
So
18
Aug
2019
OEIS, sieved primth recurrence

Am Bubo-OL-Mehrtägeler in Slowenien trug ich die Startnummer 277.
Natürlich habe ich sofort nachgeschaut, ob das eine Primzahl ist.
Es ist eine Primzahl und besser: es ist die 59. Primzahl und diese 59 ist auch eine Primzahl.
Wenn man diesen Prozess umkehrt, nämlich die n.te Primzahl nachsehen geht und mit ihrem Wert m die m.te Primzahl nachsehen, u.s.w., so entsteht eine Serie von ganzen Zahlen, wie sie in der Online Encyclopedy for Integer Series OEIS oft festgehalten wird.
Ich wollte sie dort eintragen und musste feststellen, dass 1965 schon ein anderer die Serie entdeckt hatte. Es ist A007097 und sie heisst „primth recurrence“.
https://oeis.org/draft/A007097
Achtung dieser Link geht nur mit dem Browser FireFox.
Ich habe nicht locker gelassen und eine andere Serie vorgeschlagen.
Es ist A309649 und sie heisst „Sieved primth recurrence“. Ich bin neugierig, ob der Vorschlag akzeptiert wird.
On the base of A007097 the "primeth recurrence" apply some sieve. Delete the elements of A007097 in the prime numbers and take the smallest prime left. Start a new primeth recurrence series with this number as starting element. Delete these new numbers from the primes. Retain all these smallest elements. The resulting series is 1 7 13 19 23 29 37 43 47 53 ... The next missing prime is 109.
First term a(1)=1 For the 2nd term: take all primes and delete the primes from the sequence A007097 : 1,2,3,5,11,31,127, .. This gives: 7,13,17,19, .. (1) The smallest term is 7. Our a(2)=7. Now construct an A07097 series with the starting term 7 instead of 1. The 7th prime is 17. The 17th prime is 59. the 59th prime is 277. The numbers to delete from series (1) are 7,17,59,277 .. This gives: 13,19,23,29,.. (2) The smallest term now is 13. Our a(3)=13. The next A00797 like series starting with 13 is the following. 13,41,179,.. which we delete from (2). This gives: 19,23,29,.. (3) The smallest term now is 19. Our a(4)=19. And so on.
https://oeis.org/draft/A309649
Achtung dieser Link geht nur mit dem Browser FireFox.
Mein Vorschlag ist akzeptiert worden. A309649 ist kein Draft mehr. Aber es hat sich herausgestellt, dass meine kompliziert entworfene Sequenz 1, 7, 13, 19 .. bis auf die ersten beiden Terme gleich ist der Sequenz A088982, der Primzahlen mit zusammengesetztem Index, 2, 7, 13, 19 .. oder gleich der Sequenz A007821, der Primzahlen, die zwischen den Primzahlen mit Primindex stehen, 7,13,19 ..
Sa
17
Aug
2019
Gärstenhorn
Fr
16
Aug
2019
22 spezielle Bäume im Kanton Fribourg

In der Liberté wurde berichtet, dass man 22 spektakuläre Bäume im Kanton Fribourg ausgewählt habe.
Ich habe folgenden Link gefunden, in dem man beliebig zoomen kann.
In der Folge habe ich alle 22 Bäume aufgesucht und photographiert. Begleitet hat mich Werner Straumann. Da gab es noch Herrn Pompini und Vincent Schouwey, die der gleichen Passion frönten.
Später in Slowenien in Lokve hat man mir weitere drei spektakuläre Bäume (über 40 m hoch) ans Herz gelegt, die ich auch photographieren gegangen bin.
Do
15
Aug
2019
Dieser Orientierungslaufsommer 2019 hatte 4 Elemente

Der Bubo-Mehrtage-OL in Lokve Slowenien.
Der OO-Cup in der Gegend von Bled in Slowenien.
Die Swiss-O-Week mit 6 Wettkämpfen in der Gegend von Gstaad.
Der Aargauer 3-Tägeler.
Mit Ausnahme des Aargauers kann man alle Karten bei Kurt Huber sehen, der in der gleichen Kategorie läuft wie ich (Herren 75).
Mi
14
Aug
2019
Reptend Primes

So verläuft die Divison 1 durch 7.
Das besondere ist, dass die Periode 142857 maximal lang ist. Alle Reste die die Division durch 7 lassen kann, tauchen auf. Unter den Primzahlen gibt es nur ca 34%, die diese Eigenschaft haben "full reptend". Das muss man sich näher ansehen. Auf Deutsch heissen diese Primzahlen „lange“ Primzahlen.
Di
13
Aug
2019
Jitterbug, zweiter Teil

Jitterbug war schon einmal ein Thema in diesem Blog hier.
Jetzt bin ich auf Ueli Wittorf gestossen, der gleich alt ist wie ich (Jahrgang 1943) und der die Jitterbug-Transformation verallgemeinert hat. Das ergibt bei ihm die faszinierenden Torsionspolyeder, einfach oder mehrfach belegt.
http://www.geometricdesign.ch/fileadmin/pdf/8_torsionskuboktaeder.pdf
Di
02
Jul
2019
Die Rosetten von Dorozinski

Tadeusz Dorozinski in Duesseldorf hat herausgefunden, dass man mit bestimmten drachenförmigen Vierecken schöne selbstähnliche 8-zählige Rosetten zusammenbauen kann. Er kombiniert die Zeichnungen auch mit den entsprechenden dualen Rosetten (Voronoi-Zellen). Es treten in diesen Rosetten sehr schöne Spiralen auf, ähnlich den botanischen Spiralen, die wir in Sonnenblumen beobachten können. Er hat mich gefragt, ob ich ihm die genaue Formel dieser Spiralen herausfinden könnte. Das habe ich gerne gemacht. Für die Rosette mit den Drachen, die zwei opponierende Winkel von 150° und 105° haben und in der Skalierung, bei der eine Drachenspitze auf dem Punkt (x,y) = (0,1) liegt, hat die logarithmische Spirale in Polarkoordinate eine sehr einfache Form, nähmlich r(w) = exp (-w/2 ), worin r der Radius und w der Winkel ist. Tadeusz hat auch eine Rosette mit einem anderem Drachen gebaut. Dieser hat zwei opponierende Winkel von 135° und 90°. Hier lautet die Formel für die Spiralkurve wie folgt r(w) = exp (-0.68093*w ).
So
30
Jun
2019
Rot und Weiss, Wildrosen in den Bergen

Wie die Farben des Wappens von Solothurn. Begegnet auf meiner Bergtour auf den Laitemaire on Chateau-d'Oex http://www.hikr.org/tour/post144138.html
Do
06
Jun
2019
4-Tage OL Romandie 2019

Di
21
Mai
2019
Die ominöse 42 bei Dreierkubiksummen

Es bleibt die 42. Das ist die ominöse Zahl, die im utopischen Roman "Hitchhikers Guide to the Galaxie" von Gard Jennings die Antwort auf die grösste Frage sein soll:
Deep Thought erklärt in der 42. Minute des Spielfilms die Zahl 42 als die errechnete Antwort auf die Frage „nach dem Leben, dem Universum und allem“ (“life, the universe and everything”).
https://de.m.wikipedia.org/wiki/Per_Anhalter_durch_die_Galaxis_(Film)
Ausserhalb dieses Romans kann man der Zahl 42 folgende Bedeutung geben.
Wenn man alle maximal zweistelligen ganzen Zahlen, nämlich 0, 1, 2, ... 98, 99, als Summe von drei Kubikzahlen von ganzen Zahlen mit Vorzeichen schreiben will (ausser diejenigen, die bei Division
durch 9 den Rest 4 oder 5 lassen, „ex“), so gelingt das heute nur noch mit 42 nicht !!!
Beispiele
1 = 1^3
2 = 1^3 + 1^3
3 = 1^3 + 1^3 + 1^3
29 = 3^3 + 1^3 + 1^3
Für die Zahl 33 wurde erst kürzlich eine Lösung gefunden. Es sind sehr sehr grosse ganze Zahlen dafür nötig.
33 = (8866128975287528)^3 + (-8778405442862239)^3 +(-2736111468807040)^3
ACHTUNG. Im September 2019 wurde eine Lösung für 42 gefunden !!!
42 = (-80538738812075974)^3 + 80435758145817515^3 + 12602123297335631^3
Ich wollte auf dem Internet die Lösungen für alle Zahlen 1, 2, ... 99 (ausser 42) eruieren, was mir nicht gelang. Ich musste sie also selber ausfindig machen. Hier sind sie.
s = a^3 + b^3 +c^3, “ex” die Ausnahmen.
|
s |
ex |
s |
a |
b |
c |
|
1 |
1 |
1 |
1 |
|
|
|
2 |
2 |
2 |
1 |
1 |
|
|
3 |
3 |
3 |
1 |
1 |
1 |
|
4 |
4 |
0 |
|
|
|
|
5 |
5 |
0 |
|
|
|
|
6 |
6 |
6 |
2 |
-1 |
-1 |
|
7 |
7 |
7 |
2 |
-1 |
|
|
8 |
8 |
8 |
2 |
|
|
|
9 |
0 |
9 |
2 |
1 |
|
|
10 |
1 |
10 |
2 |
1 |
1 |
|
11 |
2 |
11 |
3 |
-2 |
-2 |
|
12 |
3 |
12 |
-11 |
7 |
10 |
|
13 |
4 |
0 |
|
|
|
|
14 |
5 |
0 |
|
|
|
|
15 |
6 |
15 |
2 |
2 |
-1 |
|
16 |
7 |
16 |
2 |
2 |
|
|
17 |
8 |
17 |
2 |
2 |
1 |
|
18 |
0 |
18 |
3 |
-2 |
-1 |
|
19 |
1 |
19 |
3 |
-2 |
|
|
20 |
2 |
20 |
3 |
-2 |
1 |
|
21 |
3 |
21 |
-14 |
-11 |
16 |
|
22 |
4 |
0 |
|
|
|
|
23 |
5 |
0 |
|
|
|
|
24 |
6 |
24 |
2 |
2 |
2 |
|
25 |
7 |
25 |
3 |
-1 |
-1 |
|
26 |
8 |
26 |
3 |
-1 |
|
|
27 |
0 |
27 |
3 |
|
|
|
28 |
1 |
28 |
3 |
1 |
|
|
29 |
2 |
29 |
3 |
1 |
1 |
|
30 |
3 |
30 |
-283059965 |
-2218888517 |
2220422932 |
|
31 |
4 |
0 |
|
|
|
|
32 |
5 |
0 |
|
|
|
|
33 |
6 |
33 |
8866128975287528 |
-8778405442862239 |
-2736111468807040 |
|
34 |
7 |
34 |
3 |
2 |
-1 |
|
35 |
8 |
35 |
3 |
2 |
|
|
36 |
0 |
36 |
3 |
2 |
1 |
|
37 |
1 |
37 |
4 |
-3 |
|
|
38 |
2 |
38 |
4 |
-3 |
1 |
|
39 |
3 |
39 |
1344763 |
1173673 |
−159380 |
|
40 |
4 |
0 |
|
|
|
|
41 |
5 |
0 |
|
|
|
|
42 |
6 |
0 |
? |
? |
? |
|
43 |
7 |
43 |
3 |
2 |
2 |
|
44 |
8 |
44 |
8 |
-7 |
-5 |
|
45 |
0 |
45 |
4 |
-3 |
2 |
|
46 |
1 |
46 |
-2 |
3 |
3 |
|
47 |
2 |
47 |
-8 |
6 |
7 |
|
48 |
3 |
48 |
4 |
-2 |
-2 |
|
49 |
4 |
0 |
|
|
|
|
50 |
5 |
0 |
|
|
|
|
51 |
6 |
51 |
-796 |
602 |
659 |
|
52 |
7 |
52 |
60702901317 |
23961292454 |
-61922712865 |
|
53 |
8 |
53 |
5 |
-4 |
-2 |
|
54 |
0 |
54 |
3 |
3 |
|
|
55 |
1 |
55 |
4 |
-2 |
-1 |
|
56 |
2 |
56 |
4 |
-2 |
|
|
57 |
3 |
57 |
4 |
-2 |
1 |
|
58 |
4 |
0 |
|
|
|
|
59 |
5 |
0 |
|
|
|
|
60 |
6 |
60 |
5 |
-4 |
-1 |
|
61 |
7 |
61 |
5 |
-4 |
|
|
62 |
8 |
62 |
4 |
-1 |
-1 |
|
63 |
0 |
63 |
4 |
-1 |
|
|
64 |
1 |
64 |
4 |
|
|
|
65 |
2 |
65 |
4 |
1 |
|
|
66 |
3 |
66 |
4 |
1 |
1 |
|
67 |
4 |
0 |
|
|
|
|
68 |
5 |
0 |
|
|
|
|
69 |
6 |
69 |
-4 |
2 |
5 |
|
70 |
7 |
70 |
-21 |
11 |
20 |
|
71 |
8 |
71 |
5 |
-3 |
-3 |
|
72 |
0 |
72 |
4 |
2 |
|
|
73 |
1 |
73 |
4 |
2 |
1 |
|
74 |
2 |
74 |
−284650292555885 |
66229832190556 |
28345010569772 |
|
75 |
3 |
75 |
435203083 |
-435203231 |
4381159 |
|
76 |
4 |
0 |
|
|
|
|
77 |
5 |
0 |
|
|
|
|
78 |
6 |
78 |
-55 |
26 |
53 |
|
79 |
7 |
79 |
-33 |
-19 |
35 |
|
80 |
8 |
80 |
8 |
-6 |
-6 |
|
81 |
0 |
81 |
198873 |
191554 |
-246040 |
|
82 |
1 |
82 |
-11 |
-11 |
14 |
|
83 |
2 |
83 |
4 |
3 |
-2 |
|
84 |
3 |
84 |
41639611 |
-41531726 |
-8241191 |
|
85 |
4 |
0 |
|
|
|
|
86 |
5 |
0 |
|
|
|
|
87 |
6 |
87 |
−180751987188142 |
403046204154953 |
1800815021876303 |
|
88 |
7 |
88 |
5 |
-4 |
3 |
|
89 |
8 |
89 |
-7 |
6 |
6 |
|
90 |
0 |
90 |
5 |
-3 |
-2 |
|
91 |
1 |
91 |
4 |
3 |
|
|
92 |
2 |
92 |
4 |
3 |
1 |
|
93 |
3 |
93 |
-5 |
-5 |
7 |
|
94 |
4 |
0 |
|
|
|
|
95 |
5 |
0 |
|
|
|
|
96 |
6 |
96 |
-22 |
14 |
20 |
|
97 |
7 |
97 |
5 |
-3 |
-1 |
|
98 |
8 |
98 |
5 |
-3 |
|
|
99 |
0 |
99 |
5 |
-3 |
1 |
Mo
20
Mai
2019
Bahnen am Firmament

Ich habe mir mit dem Programm GreatStella für Polyeder einen Behelf verschafft.
Anhand dieser Animationen kann man zum Beispiel folgendes herausfinden
° Im Winter steigt der Mond am meisten ueber den Horizont.
° Im Fruehling steigt der zunehmende Mond am meisten ueber den Horizont.
° Im Fruehling steigt der abnehmende Mond am wenigsten ueber den Horizont.
° Im Herbst steigt der abnehmende Mond am meisten ueber den Horizont.
° Im Herbst steigt der zunehmende Mond am wenigsten ueber den Horizont.
Das Benutzen einer App, die die Mondbahn am Sternenhimmel zeigt, ist KEINE Lösung. Das Erfühlen gelingt nicht.
Di
12
Mär
2019
Die Cap's Familie
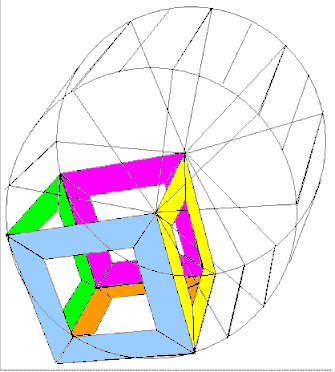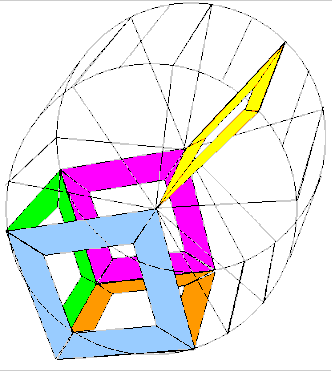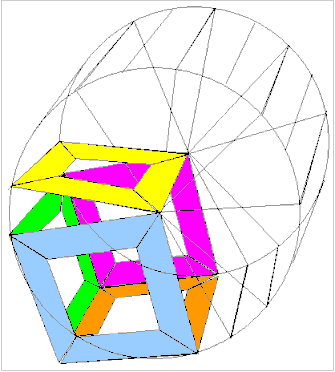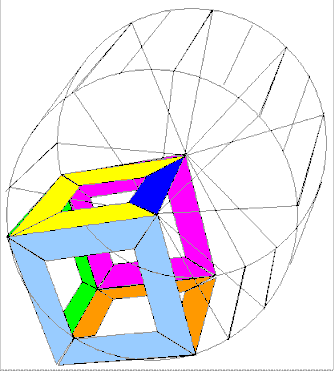
Jeder
kennt das Schiebespiel mit den 15 Zahlen und einem Loch.
Wenn man nicht in der Ebene bleibt, sondern auf eine Polyederflaeche geht und zusaetzlich eine zum Loch benachbarte Seite nicht ins Loch hineinschiebt sondern hineinklappt, bekommt man ein
faszinierendes Spiel.
Man sorgt fuer den "Durchblick", indem man die Seiten durchloechert. Weiter zerlegt man den Rest der Seite in Stuecke parallel zu den Kanten.
Beim Hineinklappen ins Loch wird nur genau eines der Stuecke umgefaerbt. Dasjenige das an der Klappachse liegt.
Die animierte Illustration zeigt den Fall eines Wuerfels.
Der Spieleerfinder hat diese Idee fuer vier Polyeder angewendet. Den Wuerfel, das Dodekaeder, das Tetraeder und das unterteilte Tetraeder. Er nennt die vier Spiele CubeCap, DodecaCap,
simpleTetraCap und TetraCap.
Ziel des Spieles ist es, alle Stuecke umzufaerben.
Diese Spiele sind erstaunlich schwierig und ich bezweifle, dass der Spieleerfinder das gewusst hat.
Ich habe jedes dieser vier Spiele im Detail analysiert und je eine Loesungsstrategie gefunden, indem ich das Spiel in einer Excel-Datei simuliert habe, wobei jedes Stueck eine individuelle Nummer
bekam. Diese Stücke sind im Originalspiel anonym.
Do
07
Feb
2019
Die Baumann'schen Zahlen und der goldene Schnitt

Der goldene Schnitt ist die Verhaeltniszahl 1.618 und taucht auf wundervolle Art an sehr viel total unterschiedlichen Stellen in der Mathematik auf. Es gibt viele Buecher nur fuer diese einzige
Zahl. Wenn man bei einem Rechteck ein Quadrat abschneiden kann und das restliche Rechteck das gleiche Seitenverhaeltnis behaelt, ist dieses Rechteck golden.
In der Folge hat man auch andere Verhaeltniszahlen untersucht. Das "silberne" Verhaeltnis, das "Plastik"-Verhaeltnis, das "supergoldene" Verhaeltnis u. s. w.
Alle diese Zahlen kann man durch eine Gleichung definieren, von denen sie eine Loesung sind. Beispiel: x*x = x + 1. Wenn ich hier fuer die Unbekannte x den Wert 1.618 einsetze stimmt die
Gleichung. Es ist also die Gleichung zur goldenen Zahl.
Ich gehe jetzt von einer ganzen Familie von Gleichungen aus, die folgende Form haben. x^5 = x^4 + x^3 + x*x + x + 1. Dies kuerze ich ab zu g54321. Wenn ein Term fehlt, wird er in der Abkuerzung
nicht erwaehnt. Beispiel: x*x = x + 1 ist g21.
Die Loesungen zu all diesen Gleichunge bekommen den gleichen Namen. Es sind die baumann'schen Zahlen. Die baumann'sche Zahl g21 ist die goldene Zahl.
Mit modern Symbolrechnerprogrammen wie Mathematica kann man alle diese Zahlen bequem herausfinden und mit beliebig viel Stellen nach dem Komma. Damit kann man auf SLOX Jagd gehen (self localising
strings = s loc s = slocs = SLOX).
Unten ("mehr lesen") folgt eine Tabelle dieser SLOX (ohne gold, plastik und supergold weil anderswo publiziert).
Mi
06
Feb
2019
DIN Musik

Ein A4-Blatt ist uns allen wohlvertraut. Es ist 29 cm hoch und 21 cm breit. Es handelt sich um eine DIN Norm (deutscher Institut fuer Normen). Durch fortlaufendes Halbieren bleibt das Seitenlaengenverhaeltnis erhalten. Dazu muss dieses den Wert 0.7071.. haben. Es ist das Inverse der Wurzel aus 2. DIN Null erfuellt zusaetzlich die Bedingung, das es genau eine Flaeche von einem Quadratmeter hat.
Das alles spielt sich in der 2-dimensionalen Ebene ab. Heinrich Hemme hatte die Idee das Ganze fuer drei Dimensionen zu verallgemeinern. Das Blatt wird dann ein Quader (ein Backstein).
Welche drei Ausdehnungen muss dieser haben, damit er seine Form nicht verliert, wenn man ihn halbiert? Nun es ist eins, dann das Inverse der dritten Wurzel aus 2, was 0.7937.. ist. Die kleinste
Ausdehnungen ist dann noch das Quadrat dieser letzten Zahl, naemlich 0.6299.. Das Halbieren geht so: nimm die groesste Ausdehnungen und halbiere sie. Das wird dann die kleinste Ausdehnungen und
die anderen zwei ruecken einen Platz nach oben.
Wenn man das Spiel auch fuer das 12-Dimensionale macht, muss man analog einen Verkuerzungsfaktor von zwoelfte Wurzel aus zwei anwenden, der das Inverse der zwoelfte Wurzel aus zwei ist!
Das ist der Wert yyyy = 0.9438.. Also eins, dann yyyy, dann yyyy^2, dann yyyy^3 u.s.w. Halbieren geht wie oben: nimm die groesste Ausdehnungen und halbiere sie. Das wird dann die kleinste
Ausdehnung und die anderen elf ruecken einen Platz nach oben.
Wenn man 440 Hertz als ersten Wert nimmt (das ist die Klangnote La) und den Verkuerzungsfaktor yyyy anwendet bekommt man Sol+ (Sol Kreuz). Das geht so weiter bis man bei La Kreuz und dann bei der
zwoelften Verkuerzung bei 220 Hertz ankommt. Das ist das eine Oktave tiefere La.
Man kann also die 12 Ausdehnungen eines beim Halbieren die Form behaltenden 12-dimensionalen Quaders mit den 12 Halbtoenen einer Oktave beschriften!
Das ist Musik!
Siehe auch den Artikel von Heinrich Hemme hier
„mehr lesen“ drücken!
Di
05
Feb
2019
Virtueller Diamant

Ich habe eine durchaus angenehme Erfahrung gemacht. Nachdem mir auf dem Auto meines Goldschmiedfreundes ein schlichtes Logo in Form eines Brillianten aufgefallen war, wollte ich die genaue Geometrie eines Brillianten in Erfahrung bringen und ihn virtuell funkeln lassen. Ich fand auf Internet tatsaechlich PovRay (ein Ray Tracing Programm) Code, der die 58 Facetten eines Brillianten beschreibt. Ich brauchte nur noch die Materialeigenschaft Glas anzugeben, die Kamera zu positionieren und Lichtquellen zu waehlen. Schon funkelte das Ding!
Sa
15
Sep
2018
Klettersteig Tour d'Ai

In diesem wunderbaren nicht enden wollenden Sommer sind wir noch auf die Tour d'Ai gestiegen und zwar vom Lac de Hongrin aus (Norden).
Hier der Bericht.
Mi
29
Aug
2018
Color number of the plane (CNP)

Jeder sollte wissen, dass man erst vor wenigen Jahren beweisen konnte, dass alle geographischen Karten mit nur 4 Farben gefärbt werden können (Vierfarbentheorem).
Ein anderes ähnliches Problem ist noch nicht gelöst.
Wieviele Farben braucht es, wenn man die unendlich ausgedehnte Ebene so anfärben will, dass zwei Punkte immer verschieden farbig sind, wenn die Distanz zwischen ihnen eins ist?
Es geht um die Color number of the plane (CNP).
In der Illustration wird gezeigt, dass diese Anzahl kleiner gleich 7 ist. Die Kachelung mit Sechsecken, deren Diagonale etwas kleiner ist als eins, hat nur 7 Farben und man erkennt, dass zwei beliebig gewählte Orte mit Distanz eins nie gleiche Farbe haben.
Der andere Teil der Illustration ist eine Moser-Spindel. Das ist ein sehr kleiner Graph mit Kanten der Länge eins, bei dem es 4 Farben braucht, um zu vermeiden dass zwei benachbarte Knoten die gleich Farbe haben.
Mit anderen Graphen, die aber viel komplizierter sind, hat man erst kürzlich beweisen können, dass es mindestens 5 Farben braucht. Zunächst hatte der Graph 1581 Knoten. Dann konnte man das auf 553 Knoten verbessern.
Die Frage bleibt also offen, ob die gesuchte Anzahl Farben 5, 6 oder 7 beträgt.
So
19
Aug
2018
Ferrata Dames Anglaises

Die 1100 Meter Anstieg zur Huette Pierredar haben wir in absolut denkwuerdigem STROEMENDEM Regen absolviert. Wir waren dann sehr froh um den warmen Empfang in der Huette.
Am Samstag hatten wir schliesslich praechtiges Wetter fuer den Klettersteig.
Do
16
Aug
2018
Schweben

Do
16
Aug
2018
Orientierungslaufen in Lettland

Do
16
Aug
2018
Ist es die kleinste?

Es besteht der Verdacht, dass 78577 die kleinste Zahl k ist, die in der Formel k*2^n + 1 vor Primalitaet schuetzt (Sierpinski).
Von nur noch 17 kleineren Zahlen war noch kein n bekannt, das Primalitaet liefert. Jetzt sind es sogar nur noch 5.
Die internationale Organisation BOINC (PrimeGrid) erlaubt einem, hier mitzurechnen. Man bekommt ein Zahlenpaar (k,n) zugeordnet, fuer das man nachweisen muss, dass es zusammengesetzt (NICHT prim)
ist. Dies geschieht mit dem Lukas-Lehner Test, der fuer diese bei n ungefahr 25 Millionen circa 7 Millionen Ziffern grosse Zahl (also ein ganzes Buch fuellend) etwa 20 Tage dauert. Ich
persoenlich habe folgende 15 Paare (k,n) abgearbeitet.
k n
24737 25704631
55459 25703434
55459 25690486
24737 25639591
24737 25586623
55459 25586158
55459 25585066
55459 25507954
24737 25455391
55459 25455298
55459 25458394
55459 25381126
21181 25307132
24737 25303807
55459 25301638
Es bleiben noch Millionen andere n zu testen und die Menschheit kann nicht sicher sein, dass es ihr gelingt, fuer die 5 uebrig bleibenden k ein geeignetes n zu finden, das eine Primzahl
liefert.
So
15
Jul
2018
Eine weitere Orientierungslaufwoche dieses Jahr: Dänemark

Es handelte sich um die Weltmeisterschaft für Senioren WMOC 2018-07-15
Am Tage des Sprints-Finals in Kopenhagen erstieg ich auch den speziellen Turm der Frelser-Kirche mit der Wendeltreppe aussen.
Impressionen in den Bildern.
Mi
13
Jun
2018
5 Orientierungsläufe im Tessin

Vom 7. bis 13.Mai 2018 nahm ich an einem 5-Tage-OL im Tessin teil. Er wurde parallel zur Europameisterschaft durchgeführt. OL im Tessin ist immer sehr fein. Darunter war auch ein Sprintlauf im Dorf Tesserete, bei dem ich erst im nachhinein erfuhr, dass er als Schweizermeisterschaft gewertet wurde, was zur Folge hatte, dass ich unbekümmert eine Rekordanzahl von Punkten holen konnte. Am Ruhetag habe ich zum ersten mal in meinem Leben mit 75 Jahren Swiss Miniature besucht. Ich habe es sehr genossen.
So
10
Jun
2018
Drei Orientierungsläufe im Wallis

Ich bin gerade zurück von einem schönen verlängerten Orientierungslauf-Weekend im bergigen Wallis.
Erste Etappe war auf dem Col des Planches. Die Zweite (ein sehr langer OL) auf dem benachbarten Col de Lein. Da fand gleichzeitig auch ein Kuh-Wettkampf statt! Am Sonntag liefen wir etwas oberhalb von Finhaut. Zum Teil sehr wildes Gelände mit riesigen Felsformationen.
Mo
04
Jun
2018
Bachwandern

Bachwandern kann wunderbar schön sein. Das habe ich erst jetzt (mit 75 Jahren) erfahren. Anlässlich der Circulissima von letztem Jahr ist dieses Projekt entstanden. Wir querten östlich von Schwarzenburg den Dorfbach auf einem sehr versteckten Steig. Von da aus konnte ich den weiteren Verlauf des Dorfbaches Richtung Osten erahnen. In einem grossen S-Mänder hat sich der Dorfbach in einem steilen Tobel nach Osten durchgegraben, um sich in das Schwarzwasser zu ergiessen. In diesem Tobel sind auf der 25000-er Karte keinerlei Wege eingetragen. Das hat mich gereizt. Das wollte ich erkundigen. Am Sonntag sind wir voller Sorge von unten her in das Tobel eingestiegen und wussten gar nicht wie weit wir kommen würden. Und dann kam die äusserst angenehme Ueberraschung, dass sich eine wunderschöne Bachwanderung von etwa 2 Stunden ergab. Die kleineren Bäche haben praktisch kein Geröll. Durch die häufigen Gewitter einer ganzen Woche war der geschliffene Sandstein wunderbar von allen Algen befreit. Ich habe Bilder auf die Hikr-Plattform gegeben.
Do
12
Apr
2018
SLOX- Jagd II

Ich habe hier die SLOX schon einmal eingeführt. Es sind sich selber lokalisierende Zahlenfolgen in einer Dezimaldarstellung. "Selflocalising strings". Beispiel die Ziffernfolge 1670 befindet sich an 1670 ter Stelle nach dem Komma in der Zahl Pi. Auf meiner ersten Jagt nach solchen SLOX hatte ich mir die Zahlen Pi, e, gamma, Phi unter anderem vorgenommen. Voraussetzung ist, dass ich einen geschlossenen Ausdruck, eine Formel, für die Zahl habe. Dann kann ich nämlich im Programm Maple beliebig viel Stellen nach dem Komma bestellen. Wenn ich keine Formel, aber ein Polynom mit ganzzahligen Koeffizienten habe und die interessierende Zahl eine Wurzel dieses Polynoms ist (d.h. den Polynomwert zu Null werden lässt), dann liefert Maple auch beliebig viele Stellen. Bei dem hier gezeigten Polyeder wurden mir 21 Polynome zugeschickt, von denen je eine Wurzel eine Zahl liefert, mit denen ich alle Koordinaten des Polyeders ausrechnen kann. In diesen 21 Zahlen habe ich ALLE SLOX gesucht, die kleiner als 10000 sind. Hier ist die Tabelle.
Sa
07
Apr
2018
Die Boy-Fläche

Die Boy-Fläche ist enorm attraktiv und von bildenden Künstlern oft aufgegriffen worden. Es gibt sehr viele Skulpturen auf der Welt. Wenn man mental ein Möbiusband und eine Scheibe dem Rand nach zusammennäht, bekommt man diese Fläche. Natürlich geht das nicht gut und es braucht Durchdringungen. Mit den modernen heutigen Mitteln (Computeranimationen) kann man dieses verdrehte Ding dem Publikum viel näher bringen.
Die Boy-Fläche ist aequivalent zur Projektiven Ebene. Heute kann man fast nicht mehr behaupten, dass das zur Allgemeinbildung gehört. Siehe hierzu folgendes: https://m.youtube.com/watch?v=mFC0qdrpip0
Neugierig gemacht? Auf dem Internet findet ihr jede Menge an Infos über die „Boy Surface“.
Mo
05
Mär
2018
Die Figur eines Knotens fliegen

Seit laengerer Zeit schon beschaeftigt mich diese Idee. Natuerlich darf es der einfachste der Knoten sein, ein Kleeblattknoten. Ich stelle fest, dass diese Idee in allen Flugakkrobatikprogrammen und Wettbewerben nicht vorkommt. Natuerlich kommt auch ein Modellflugzeug in Frage. Oder sogar ein auf einem Rechner simuliertes Fliegen oder Modellfliegen. Zur Sichbarmachung waere ein Kondensstreifen oder eine Rauchfahne angenehm. Mental habe ich zuerst zwei vertikale Loopings ins Auge gefasst, die etwas gegeneinander verdreht sind. Das ergibt eine fluessige Bewegung. Als ich schlussendlich jemand motivieren konnte, geschah das in einer Sporthalle (Michel Gassmann in Schmitten), wo die Hallenhoehe die zwei Loops nicht erlaubte. Die Kombination einer horizontalen Oese, durch die dann vertikal mit einem Loop geflogen wurde, erwies sich am praktischsten. Diese Anlage eines Knotens kann dadurch gesteigert werden, dass die horizontale Oese zweifach geflogen wird. Dann ergibt sich der Torusknoten 5-1. Aequivalent dazu waere eine horizontale Oese und mehrfache Loops durch die Oese. Der Blickfang hier zeigt den Knoten mit einem Bergseil. Ich habe den Flug in der Sporthalle gefilmt und der Film kann hier https://youtu.be/aWor5SNS79g angesehen werden.
Fr
02
Mär
2018
Slox-Jagd

Vor etwa einer Woche habe ich meinen ersten SLOX zu Gesicht bekommen. Wisst Ihr, was da ist? Ein Self-LOCalising String, also SLOCS, modern geschrieben SLOX (String = Ziffernfolge). Es war ein besonders grosser : 79873884 (fast 80 Millionen). Er tritt in der Zahl Pi auf und zwar, wie es sich fuer einen Slox gehoert genau an der 79873884ten Stelle nach dem Komma. Die Slox sind nicht so haeufig. Obiger Slox ist nur der vierte in Pi. Die bisher bekannten Slox in Pi sind hier aufgelistet http://oeis.org/A057680. Mit einem kleinen Maple-Programm bin ich selber auf die Slox-Jagd gegangen. Ich habe andere Zahlen als Pi angschaut: e, gamma, die metallischen Konstanten gold, silber, bronze und plastic. Dann auch 3 Splits von Polygonen in gleichflaechige Stuecke T2, S3 und P2, bei denen ich ueber eine geschlossene Formel verfuege. Dito fuer 6 Zylinderschnitte 3, 4, 6, 6k, 7 und 10. Des weiteren habe ich die Slox in Pi im Oktal- statt im Dezimalsystem angeschaut. In den folgenden Bildern könnt Ihr meine Beute sehen (Drauf klicken zum Vergrössern).
Fehler: Die zweite SLOX von Pi ist nicht 1670 sondern 16470.
Mi
14
Feb
2018
Ein Mondglobus

Ich habe unheimlich viel Spass an diesem Mondglobus. Er wurde in 3D-Printing hergestellt. Ich habe das grösste Exemplar genommen. Ich kann sogar meine Lieblingstrukturen „Rupes recta“ und „Montes recti“ erkennen. Ich warte gespannt auf die Erhältlichkeit von einem entsprechenden Mars-Globus, einem Pluto-Globus und einem Enceladus-Globus. Der Verzicht auf irgendwelche Beschriftungen ist entscheidend. Die Idee das Profil zu invertieren, um die dunklen Mare durch Abschattung zu erzielen, ist genial.
Sa
16
Dez
2017
Melinda's Erfindung

Melinda Green lebt in Kalifornien und hat eine phantastische Erfindung gemacht. Zumindest fuer Eingeweihte. Es handelt sich um ein materielles Aequivalent des vierdimensionalen Rubikwuerfels mit Seitenlaenge zwei. Ein solches hatte man lange Zeit zu recht fuer unmoeglich gehalten. Es ging denn auch nur unter Zuhilfenahme von Magneten (die heute gut 10 mal staerker sind als noch vor 40 Jahren). Melinda ist Mitglied eines Internetforums "4D cubing" von Yahoo, bei dem ich auch mitmache. Sie hat mir die Nummer 1 einer kleinen Serie geschickt, die sie bei ShapeWays printen laesst und dann selber zusammenbaut. Entscheidend bei der Erfindung war, dass man beim unverdrehten Wuerfel nicht einen einfarbigen Wuerfel drehen laesst, der Nachbarfarben mitschleppt, sondern ein Oktaeder, das die gleichen 24 Drehungen hat wie der Wuerfel. Das Modell hat eine wunderbare Haptik. Ich zeige in der Illustration den 3-dimensionalen 2x2x2 Rubik und die Erfindung von Melinda. Unter "mehr lesen" folgt eine Bildschirmansicht des 4-dimensionalen 2x2x2x2 unter anderem. Ich erinnere daran, dass der Mathologer eine wunderbare Einfuehrung in den 3x3x3x3 gemacht hat hier. Melinda's Youtube ist hier.
Do
09
Nov
2017
Circulissima 2017

Thomas Ulrich hat mir mit seiner Wiederholung der Direttissima die Idee gegeben, ebenfalls einen zu durchwandernden, 1 km breiten Korridor zu definieren. Ich habe einen Kreis mit Zentrum Fribourg und Radius 20 km gewählt. Wir haben 10 Etappen à 4h bis 5h gemacht (nicht am Stück). Etappe 1 Corbière-Mosettes, Etappe 2 Mosettes-Zollhaus, Etappe 3 Zollhaus-Riffenmatt, Etappe 4 Riffenmatt-Hängebrüggli, Etappe 5 Hängebrüggli -Schnurrimühle, Etappe 6 Schnurrimühli-Lugnorre, Etappe 7 Lugnorre - Grandcourt, Etappe 8 Grandcourt - LesMoulins, Etappe 9 LesMoulins - Liamont und Etappe 10 Liamon-Corbière. Hier ist ein Bericht mit Fotos: http://www.hikr.org/tour/post127035.html
So
05
Nov
2017
Jitterbug

Es ist recht lange her, dass die Ausstellung "Phenomena" in Zürich stattgefunden hat (1984). Am besten mag ich mich ein Gestänge (die Kanten) eines hausgrossen Oktaeders erinnern. Das Gestänge war beweglich und konnte sich kontinuierlich zu den Kanten eines Kubooktaders verändern. Das Publikum konnte eine Hebebühne in der Mitte des Polyeders betreten. Die Transformation der Kanten ist nach Jitterbug benannt. Auf Youtube gibt es Animationen dazu. Tadeusz Dorozinski hat mich nach einer genauen Beschreibung dieser Jitterbug-Transformation in analytischer Geometrie gefragt. Ich habe sie mit Vergnügen ausgerechnet. Ich habe auch ein Modell aus Karton für die Jitterbug-Transormation.
Transformation 1
https://m.youtube.com/watch?v=HekEKdcw5_k
Transformation 2
https://m.youtube.com/watch?v=FfViCWntbDQ
Phaenomena 1984
Sa
04
Nov
2017
Snub8 und Snub10

Die archimedischen Polyeder SnubWürfel und SnubDodekaeder sind meine Lieblingspolyeder. Mein Brieffreund Tadeusz Dorozinski ist mit dem Anliegen an mich herangetreten, sie wie folgt abzuändern. Statt für den SnubWürfel verkleinerte Quadrate in den Seiten eines Würfels so zu drehen, dass die sich auftuende Lücke mit gleichseitigen Dreiecken gefüllt werden kann, neu verkleinerte Achtecke zu nehmen. Es braucht dann einen anderen Drehwinkel (7.928°) und in den Würfelecken entstehen nicht gleichkantige Drachen. Ich nenne das neue Polyeder „Snub8“.
Auch beim SnubDodekaeder kann man statt der verkleinerten Fünfecke verkleinerte Zehnecke nehmen. Hier entsteht mit dem Drehwinkel (7.431°) das neue Polyeder „Snub10“.
Natürlich sind es händige Polyeder, was besonders reizvoll ist.
Mi
25
Okt
2017
Zwingherrenbogen-Wiederholungskurs
Fr
08
Sep
2017
Ein Sonnentag in einer regnerischen Woche
Sa
19
Aug
2017
Aeusseres Barrhorn 3610m

Nach 47 Jahren bin ich auf den gleichen Berg zurückgekehrt. Im Mai 1970 machte ich es mit Skiern.
Jetzt war es eine schöne Sommertour. Siehe mein Bericht in http://www.hikr.org/tour/post124228.html
Di
15
Aug
2017
OL Sommer 2017

Zuerst gings für eine Woche nach Slowenien, wo wir ganz in der Nähe der Hauptstadt Ljubiljana in den Waeldern unterwegs waren. Für mich ein prägendes Ereignis war, dass in der Schlussetappe ein Zweig mir die Brille abstreifte und ich diese nicht mehr finden konnte. Das Wiederbeschaffen einer Brille in den Optikergeschaeften von Ljubiljana war dann ein besonderes Abenteuer. Es ist heutzutage nicht leicht, ein Geschaeft zu finden, das Rohlinsen an Lager hat. Nur so kann man probieren und die Brille nach Anfertigung gleich mitnehmen. In der Zweiten Woche zog ich weiter nach Kroatien auf die Insel Cres. Obschon die beiden Länder benachbart sind, gab es nur auf Cres richtiges, heisses Mittelmeer-Ambiente. Eine Woche drauf nahm ich am Aargauer Dreitage-OL teil, der erstaunlicherweise drei schoene Läufe fast ohne gefürchtete Dornen anbieten konnte (Wettkampfzentrum in Vordemwald!). Beim OL sind natürlich nicht Postkarten sondern OL Karten die wertvollsten Erinnerungsstücke. Weil Kurt Huber in der gleichen Kategorie läuft wie ich, kann ich auf seine Berichte verweisen mit Karten in guter Auflösung (drauf klicken und zoomen!).
http://kurthu.blogspot.ch/2017/08/slowenienkroatien-tour.html
Mo
10
Jul
2017
Möglichst Runde

Polyeder mit gleichlangen Kanten beschäftigen mich weiterhin. In der Juni Nummer 2017 des Spektrum der Wissenschaft präsentiert Christoph Pöppe "unsere" Wunderwelt der Gleichkanter http://www.spektrum.de/magazin/wunderwelt-der-gleichkantigen-polyeder/1453313. Im Moment haben wir einen Wettbewerb laufen, der für alle Gleichkanter mit weniger als 123 Flächen jeweils den rundesten Kandidaten sucht. Den Stand der Dinge kann man jederzeit auf http://www.baumanneduard.ch/Galerie.pdf ansehen gehen.
So
09
Jul
2017
Umrundung der Argentine

Gestern war ich wieder einmal mit Ehemaligen von Ilford in den Bergen unterwegs. Wir waren zu fünft. Das Wetter war mit von der Partie und wir konnten die Wanderung vom 13 km mit 800m Höhenmeter rauf und dann wieder runter geniessen. Mit den Pausen waren wir 7h unterwegs. Hier könnt Ihr meinen Bericht lesen (mit viel Blumen natürlich)..
 Baumann Eduard
Baumann Eduard









